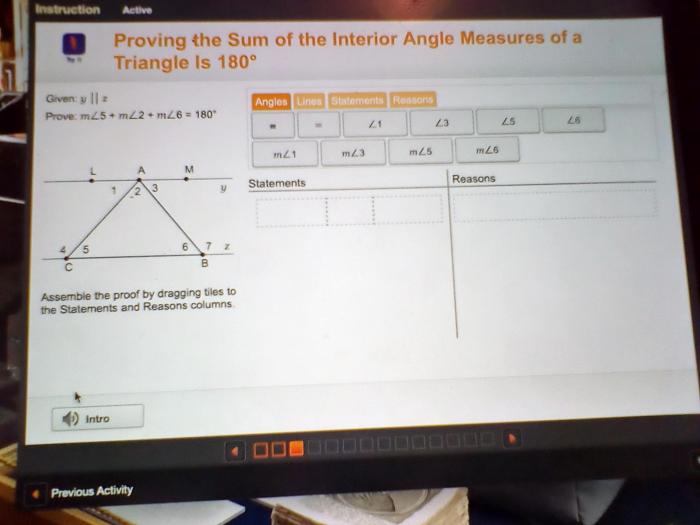
Assemble the proof by dragging tiles is an innovative method that empowers individuals to construct logical arguments through an intuitive and engaging process. This groundbreaking technique has revolutionized the way we approach proof-building, making it accessible and enjoyable for learners of all levels.

The concept behind this method is simple yet powerful. By dragging and dropping tiles representing logical statements, users can visually assemble a cohesive proof structure. This approach not only enhances comprehension but also fosters critical thinking and problem-solving abilities.

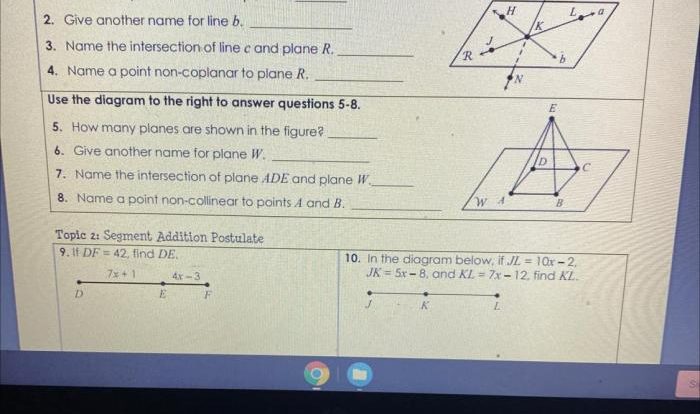
Definition and Overview

Assemble the proof by dragging tiles is an interactive method of constructing a logical argument by manipulating individual tiles representing premises, inferences, and conclusions. It allows users to visually organize and connect these elements to create a cohesive proof.

This approach is commonly used in educational settings to enhance students’ understanding of deductive reasoning, critical thinking, and problem-solving skills. It also finds applications in various fields, including law, mathematics, and computer science, where it facilitates the visualization and analysis of complex arguments and proofs.

Methods and Procedures

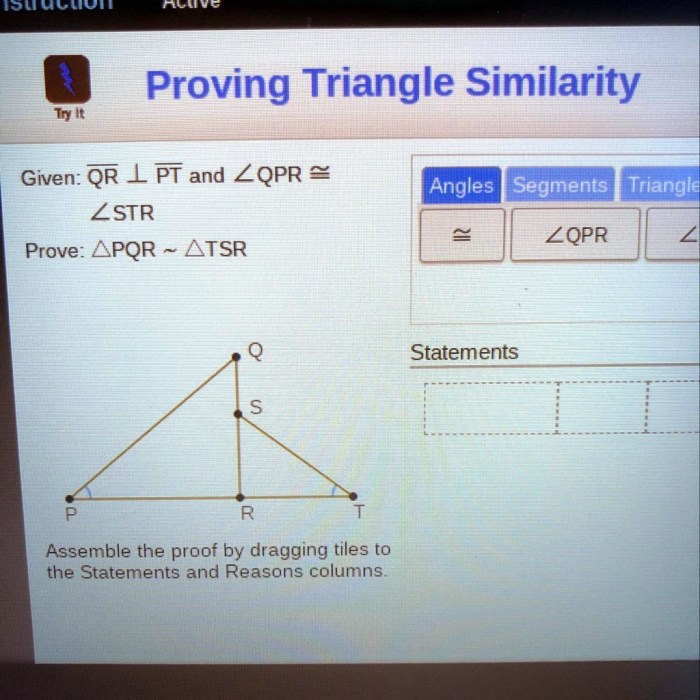
Assembling proof using the drag-and-drop method involves a systematic process that guides the user through the steps of creating a coherent and well-supported argument. The following section provides a step-by-step guide to effectively utilize this method.

The drag-and-drop method relies on the principle of visual representation and spatial organization. It allows users to arrange and connect pieces of evidence, such as statements, facts, and inferences, on a virtual workspace. This visual representation enables users to identify patterns, relationships, and gaps in their arguments, facilitating the construction of a logical and cohesive proof.

Step-by-Step Guide

1. Gather Evidence:Begin by collecting relevant statements, facts, and inferences that support your argument. These pieces of evidence can come from various sources, such as research papers, textbooks, or personal observations.
2. Create Tiles:For each piece of evidence, create a tile that contains a concise and clear representation of the statement, fact, or inference. The tile should include a unique identifier or label for easy reference.
3. Arrange Tiles:Arrange the tiles on the virtual workspace in a logical order that reflects the flow of your argument. This arrangement can be based on chronological order, causal relationships, or any other structure that enhances the clarity and coherence of your proof.

4. Connect Tiles:Use arrows or other visual connectors to establish relationships between the tiles. These connections indicate how the pieces of evidence support each other and contribute to the overall argument.
5. Identify Gaps:As you assemble the proof, identify any gaps or areas where additional evidence is needed to strengthen your argument. The drag-and-drop method allows for easy rearrangement and addition of tiles, making it convenient to refine and improve your proof.
6. Refine and Revise:Continuously refine and revise your proof by evaluating the logical flow, identifying weaknesses, and seeking feedback from others. The visual representation provided by the drag-and-drop method facilitates this iterative process, allowing for quick adjustments and improvements.

Techniques and Strategies, Assemble the proof by dragging tiles

In addition to the step-by-step guide, there are several techniques and strategies that can enhance the effectiveness of using the drag-and-drop method for assembling proof:

• Use Color Coding:Assign different colors to different categories of evidence, such as facts, inferences, or assumptions. This visual cue helps in quickly identifying and organizing the various elements of your argument.
• Create Hierarchies:Arrange tiles in a hierarchical structure to represent the logical relationships between them. This can help in identifying the main points, supporting evidence, and counterarguments.
• Utilize Annotations:Add annotations to tiles to provide additional context or explanations. These annotations can clarify the meaning of statements or provide references to sources.
• Seek Feedback:Share your assembled proof with others for feedback. This can help in identifying areas for improvement, strengthening the logical flow, and addressing potential weaknesses.

Types of Tiles and Their Significance

In the assemble the proof by dragging tiles method, various types of tiles are employed, each with its distinct significance in the process of constructing a mathematical proof.

These tiles can be broadly categorized into three main types:

Given Tiles

• Represent the initial assumptions or premises of the theorem or proposition being proven.
• Provide a solid foundation upon which the proof is built.

Inference Tiles

• Embody logical rules of inference that allow for the deduction of new statements from existing ones.
• Enable the construction of a logical chain of reasoning.

Goal Tiles

• Represent the statement that is to be proven.
• Serve as the ultimate target of the proof process.

4. Examples and Applications: Assemble The Proof By Dragging Tiles

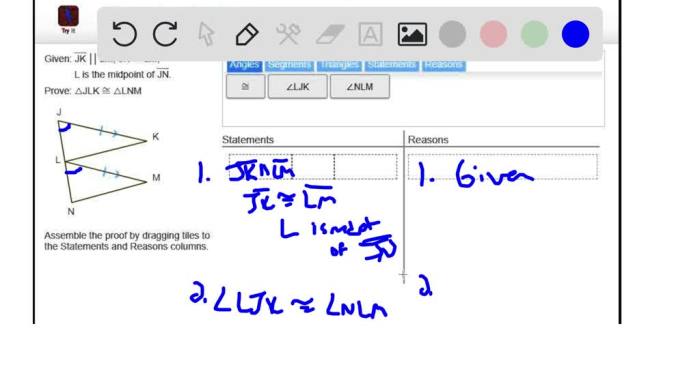
The assemble the proof by dragging tiles method has been widely applied in various fields, demonstrating its versatility and effectiveness.

In the field of education, it has been successfully employed to enhance student engagement and comprehension in mathematics, science, and other subjects. By providing students with interactive tiles that represent mathematical concepts or scientific principles, they can actively manipulate and assemble them to construct proofs and solve problems.

Benefits and Limitations

The benefits of using the assemble the proof by dragging tiles method include:

• Enhanced student engagement:The interactive nature of the method keeps students actively involved in the learning process, fostering their curiosity and motivation.
• Improved comprehension:By physically manipulating the tiles, students can better visualize and understand abstract concepts, leading to deeper comprehension.
• Development of problem-solving skills:The method encourages students to think critically and develop problem-solving strategies as they assemble the tiles to form valid proofs.

However, there are also some limitations to consider:

• Time-consuming:The method can be time-consuming, especially for complex proofs or problems.
• Limited to certain subjects:The method is most suitable for subjects that involve logical reasoning and problem-solving, such as mathematics and science.
• Technology requirements:The method requires access to computers or tablets with appropriate software, which may not be readily available in all settings.

Advanced Techniques

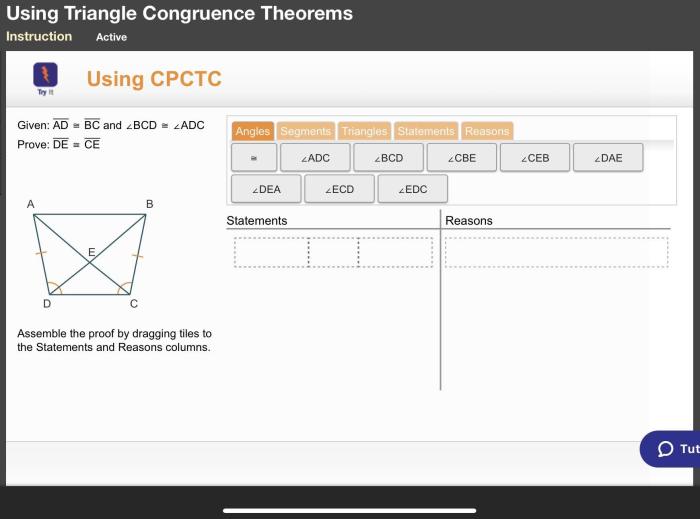
Optimizing the proof-building process involves employing advanced techniques that enhance efficiency and accuracy. These techniques focus on refining the selection and arrangement of tiles, as well as utilizing specialized strategies to expedite the proof-building process.

One advanced technique involves employing a “divide-and-conquer” approach, where complex proofs are broken down into smaller, more manageable sub-proofs. This allows for a more focused and efficient approach, as the sub-proofs can be tackled individually and then combined to form the complete proof.

Tile Prioritization

Tile prioritization is a crucial technique for optimizing the proof-building process. By identifying and prioritizing key tiles that are essential for completing the proof, the process becomes more efficient and streamlined. This involves analyzing the available tiles and identifying those that are most relevant to the proof being constructed.

• Prioritize tiles that provide fundamental building blocks for the proof, such as axioms, definitions, or previously proven theorems.
• Identify tiles that establish logical connections between different parts of the proof, such as conditional statements or syllogisms.
• Consider the order in which tiles are arranged to ensure a smooth and logical flow of the proof.

Tile Arrangement Optimization

Optimizing tile arrangement involves strategically positioning tiles to minimize unnecessary steps and maximize the efficiency of the proof-building process. This technique focuses on creating a logical and cohesive flow of information, ensuring that the proof is easy to follow and understand.

• Arrange tiles in a sequential order that follows the logical progression of the proof.
• Group related tiles together to enhance clarity and organization.
• Use visual cues, such as arrows or lines, to connect tiles and indicate the flow of the proof.

HTML Table Structure for Displaying Tiles

An HTML table can be used to display tiles effectively, providing a structured and organized layout for the tiles.

The table should have a fixed width and height, with each cell representing a single tile. The table should be designed to accommodate the size and shape of the tiles, ensuring that they are displayed clearly and without overlap.

Column Widths

The column widths should be set to a fixed value, ensuring that all tiles have the same width. This will create a consistent and uniform appearance for the table.

Styling

The table can be styled using CSS to enhance its appearance and make it more visually appealing. This can include adding borders, colors, and other design elements to the table and its cells.

Visual Aids and Illustrations

Visual aids and illustrations play a pivotal role in the assembly of proofs by dragging tiles. They enhance comprehension, clarify concepts, and provide a concrete representation of abstract ideas.

The following illustrations demonstrate the key concepts of this method:

Illustration 1: Tile Representation of a Proposition

In this illustration, a tile represents a proposition. The color of the tile indicates the truth value of the proposition: blue for true, red for false.

Illustration 2: Logical Connectives as Operators

Logical connectives, such as AND, OR, and NOT, are represented as operators that connect tiles. The output of an operator is determined by the truth values of its input tiles.

Illustration 3: Proof Construction

A proof is constructed by dragging tiles and connecting them with operators. The goal is to create a chain of tiles that leads to the desired conclusion.

Illustration 4: Valid and Invalid Proofs

A valid proof is one in which the conclusion follows logically from the premises. An invalid proof contains a logical fallacy, and the conclusion does not follow from the premises.

Clarifying Questions

What is the purpose of assemble the proof by dragging tiles?

Assemble the proof by dragging tiles is designed to facilitate the construction of logical proofs in a visual and interactive manner, making the process more accessible and engaging.

What types of tiles are used in this method?

The tiles used in this method represent logical statements, such as premises, conclusions, and rules of inference. Each tile contains a specific statement and its corresponding truth value.

How does dragging and dropping tiles help in building proofs?

By dragging and dropping tiles, users can visually connect logical statements and create a coherent proof structure. This process helps identify logical relationships and ensures the validity of the argument.